An introduction to sorting algorithms
ADVERTISEMENT
Table of Contents
- Introduction
- There is no best algorithm
- Sorting algorithms
- Stable sort vs. unstable sort
- Go big or go home
- The mid line
- Rock bottom
- Benchmark testing
- Parallel sorting
- Conclusion
Introduction
Starting with some motivation on why we need to understand the best ways of sorting data. Consider the below quote, which was said 2 years ago...
World population projected to reach 9.7 billion by 2050. The current world population of 7.3 billion is expected to reach 8.5 billion by 2030, 9.7 billion in 2050 and 11.2 billion in 2100, according to a new UN DESA report, “World Population Prospects: The 2015 Revision”, launched today. Jul 29, 2015
Hmm strange, this was also said 2 years ago:
In 2015, the International Telecommunication Union estimated about 3.2 billion people, or almost half of the world's population, would be online by the end of the year.
Yep, that's an estimated 4.1 billion people in 2015 without internet. How could they live right? Well, it's going to be an interesting future when that gap is filled and those people are Internet enabled. And it is very likely that it will become a reality, companies are working on this right now. Facebook's Internet.org is just one of these companies aiming to connect the whole world with Internet. So what happens when everyone is on the interwebs?
But what does this mean from a developer's perspective? More data to sort through.
Luckily, sorting data is a very interesting problem to solve, and there isn't always a one-size fits all solution. Sorting is really important as it makes data more readable and convenient for both users, and systems. When handling large datasets (millions and billions of files), a strategy needs to be formulated in order to solve sorting problems, while providing efficient results. Even for millions of items in a dataset, you would want to optimize your sort method for a more functional application. And you certainly don't want to add extra time to your sorting method that's for sure. There are algorithmic strategies that do pretty well against sorting large data sets, such as the divide and conquer strategy. Which is essentially, dividing the dataset into subsets, and conquering by sorting each subset and returning it to make a sorted dataset.
There is no best algorithm
There are many go-to sorting algorithms that help you sort data in different ways, each with individual qualities and trade-offs. In order to choose the right algorithm for the job, we need to know more about the sort problem itself. Also the dataset properties need to be analyzed, and understood in terms of how it needs to be sorted (lexicographical, numerical, alphabetical, customised ordering etc.).
Here are some questions to ask yourself when selecting the right one for you.
- How big is the data to be sorted? Can you fit it in main memory? Can you fit 1/2 in memory?
- Is the data already some-what sorted already?
- Will the data input grow over time?
- What system resources are available?
- What is the data type of the data? (primitives, objects, both?)
- Can we fit the data in a database?
- Are we sorting just once?
- Is there a time/space constraints?
Sorting algorithms
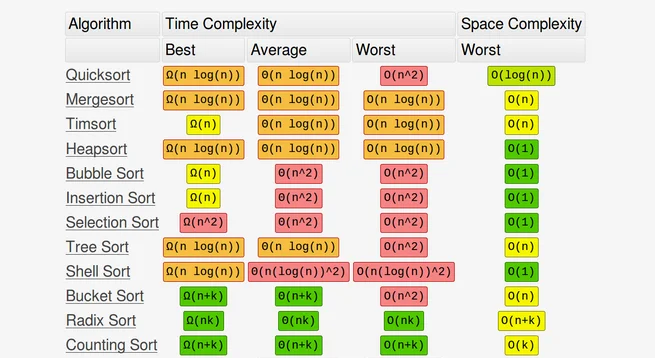
There are a large amount of implementations online, and some might not be optimal, so make sure you know exactly what the algorithm is doing. I won't be using code in this post, but rather highlighting some pros and cons to help you narrow down some algorithm choices, by addressing the above questions. Also you might want to check out the difference between best case, worst case and average case performance to help make your decision. It is important if you need an algorithm to be consistent with your performance requirements. For example, if your algorithm has a best-case of O(n log n) but a worst-case of (n^2) performance, and you might expect the amount of data input to increase ten-fold over the next year, then favoring worst-case running time will provide you with assurance that your algorithm will not lose its quality later.
Stable sort vs. unstable sort
A stable sort is a sort which guarantees that when two items are compared and determined to be the same, their positions in the set will not be compromised. Whereas for unstable sort the positions of the items may change given the nature of the sort.
Go big or go home
For large-sized datasets, we can use external sorting which is a class of algorithms that load chunks of data from secondary storage into main memory, then sorts upon it. The external merge sort is probably one of the most commonly used, as it loads the chunks of data into main memory (RAM) and sorts the chunks, merges them back together to then be written back to disk.
Another option that involves little coding is Google's BigQuery, where you all you need to do is upload your dataset, and it utilizes serverless technology saving you time setting up the infrastructure needed. You can just run a SQL (or SQL-like) query to sort your dataset. Easy as that.
The mid line
If the dataset is just big enough to fit in RAM, then we can use an internal sort that might offer greater performance benefits. Another possibility we have to take into account is to identify if the data is mostly sorted already, and if that's the case then you might want consider using a bubble sort or an insertion sort. I would suggest also to consider using a timsort, as it is a hybrid sort (combination of merge sort, and insertion sort) that runs at worst case O(n lg n). Python's built-in sort() method utilizes timsort.
Rock bottom
The general rule is to use simple sorting algorithms on small datasets. Insertion sort is a good candidate for this as it promises good performance benefits, and is extremely simple to implement. If your dataset is really small then you should weigh up just using a standard library sort() method. For example, if your application is written in Java, then Collections.sort() is probably fast enough. Which leads to the next point.
Benchmark testing
Time to dust off that profiler and put it to good use! Your algorithm is blazingly fast? But, how much space are you using? And vice versa. Benchmark testing helps you to understand and compare the performance of your algorithm.

Parallel sorting
The best worst-case time complexity for a sorting algorithm is O(n log n). But what if we could do better? What if we could split our sort algorithm into sub-problems, and solve those sub-problems simultaneously. It's possible, and it can be done by solving each sub-problem on a seperate CPU core. Among other sort methods, the merge sort can be modified to utilize parallelism to give a speed increase, it is known as a Parallel merge sort. It is a parallel algorithm that provides sorting in O(log n) worst-case running time. O(n log n) / n = O(log n). That is an incredible performance enhancement.
Conclusion
There are many sorting strategies out there, and it is about finding the best one for you. Another entirely likely possibility is the time required to sort may not be important at all. For instance, if you run into a problem where you only need to ever sort data once, then the choice of algorithm might not actually matter. Go grab a coffee and let that sort itself out. But generally speaking, sorting is performed routinely and it requires some analysis to help save time and space. On the bleeding edge, parallel sorting is being optimized in the field of high-performance computing (HPC) by using GPUs, as they have been proven worthy for general computing too!
Final Notes
Recommended product: Coding Essentials Guidebook for Developers